4.1. Khái niệm chung

Từ mô hình của hệ thống hình 3.1. Phương pháp hàm truyền đạt chuyển quan hệ phương trình vi phân thành quan hệ phân thực đại số nhờ phép biến đổi Laplace

4.1.1 Phép điến đổi Laplace

a. Định nghĩa

Cho f(t) là hàm xác định với mọi t ≥0, biến đổi Laplace của f(t) là: 


Trong đó:
s: biến phức (biến Laplace)
L: toán tử biến đổi Laplace
e-st: là hạt nhân của phép biến đổi
F(s): hàm phức
f(t): hàm biểu diễn trên miền thời gian xác định trên R
 Để thực hiện biến đổi Laplace hàm f(t) phải là hàm thực và thỏa mãn một số điều kiện sau:
- f(t) = 0 khi t < 0
- f(t) liên tục khi t ≥ 0, trong khoảng hữu hạn bất kỳ cho trước chỉ có hữu hạn các điểm cực trị
- Tích phân:    hội tụ
  b. Tính chất:
Giả thiết f(t) và g(t) là hai hàm theo thời gian có biến đổi Laplace tương ứng:
(4.3)
Tính tuyến tính
 (4.4)
Định lý trể
 (4.5)
Ảnh của đạo hàm:
Nếu hàm f(t) có biến đổi Laplace L{f(t)} = F(s) thì:
(4.6)
trong đó f(0+) là điều kiện đầu
Ảnh của tích phân:
Nếu hàm f(t) có biến đổi Laplace L{f(t)} = F(s) thì:
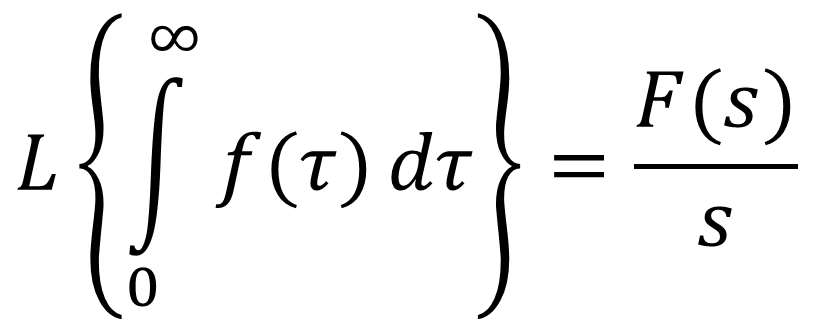   (4.7)
Định lý giá trị cuối
 (4.8)

c. Phép biến đổi Laplace của các hàm cơ bản
*   Hàm xung đơn vị (hàm dirac):
Hàm xung đơn vị thường được sử dụng để mô tả nhiễu tác động vào hệ thống:

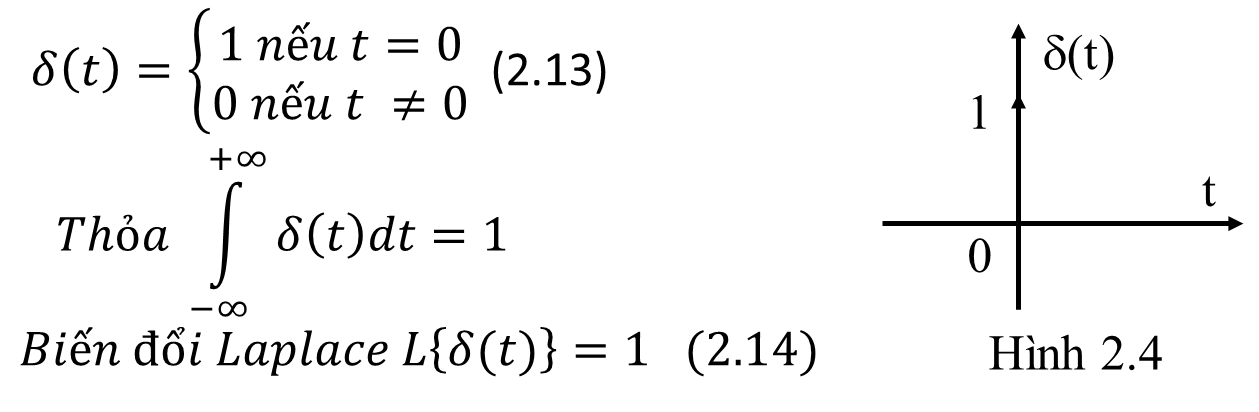
* Hàm nấc đơn vị (step): tín hiệu vào hệ thống điều khiển ổn định hóa

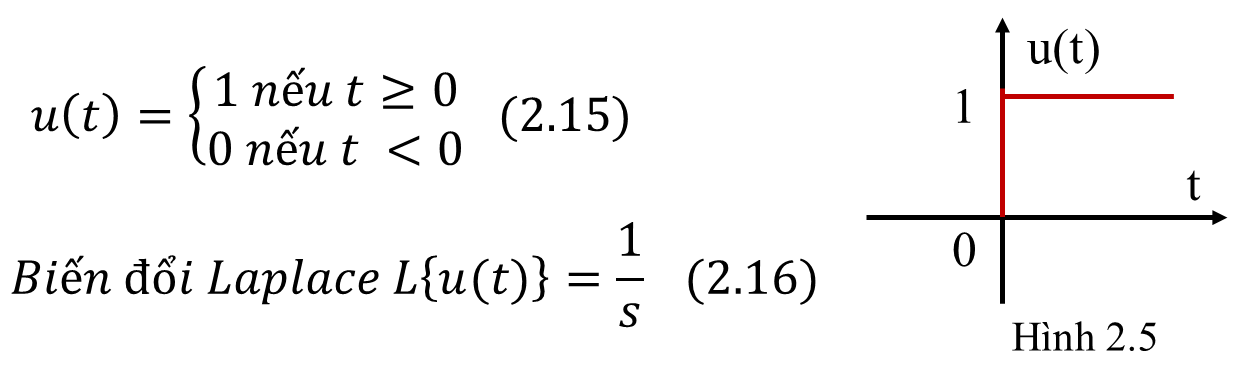
* Hàm dốc đơn vị (Ramp): tín hiệu vào hệ thống điều khiển theo dõi

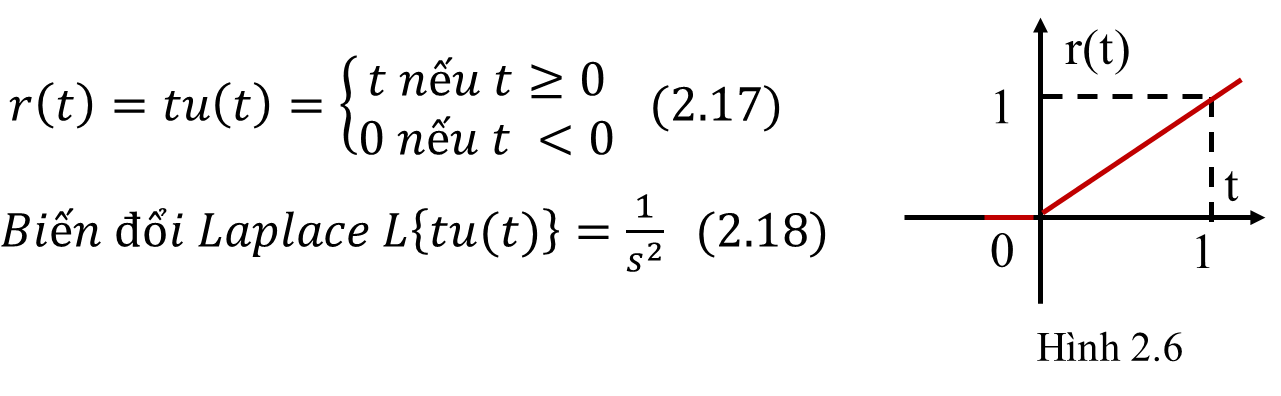
* Hàm mũ

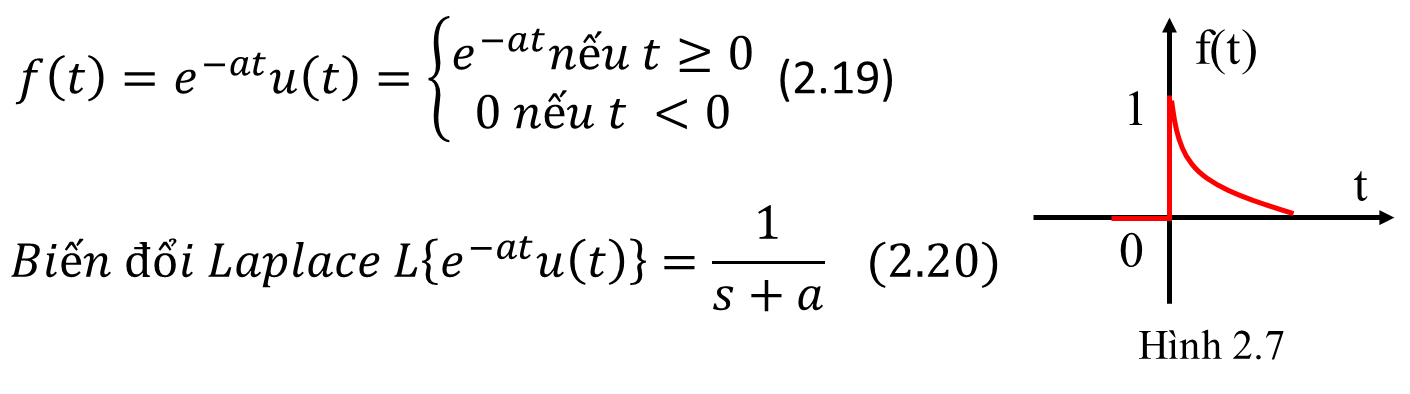
* Hàm Sine

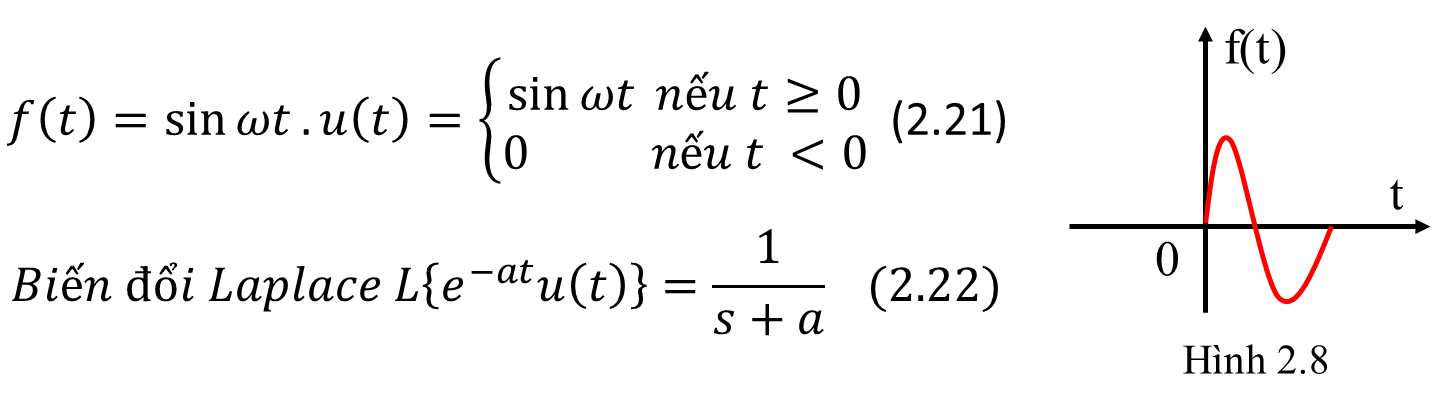
Bảng biến đổi Laplace của các hàm cơ bản:

 

 

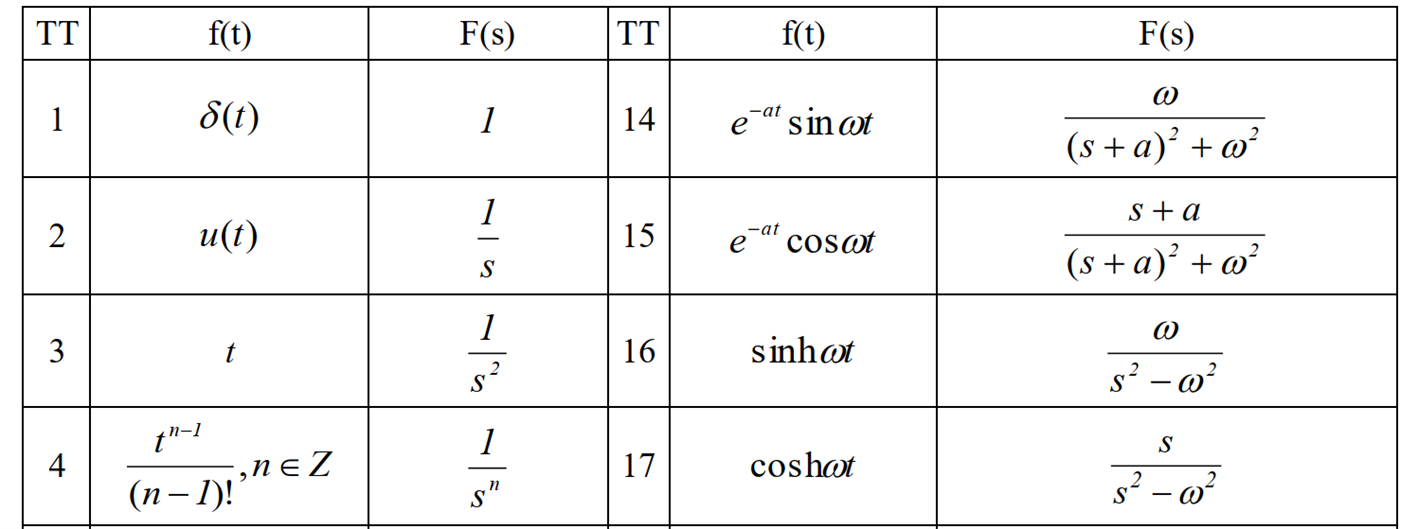
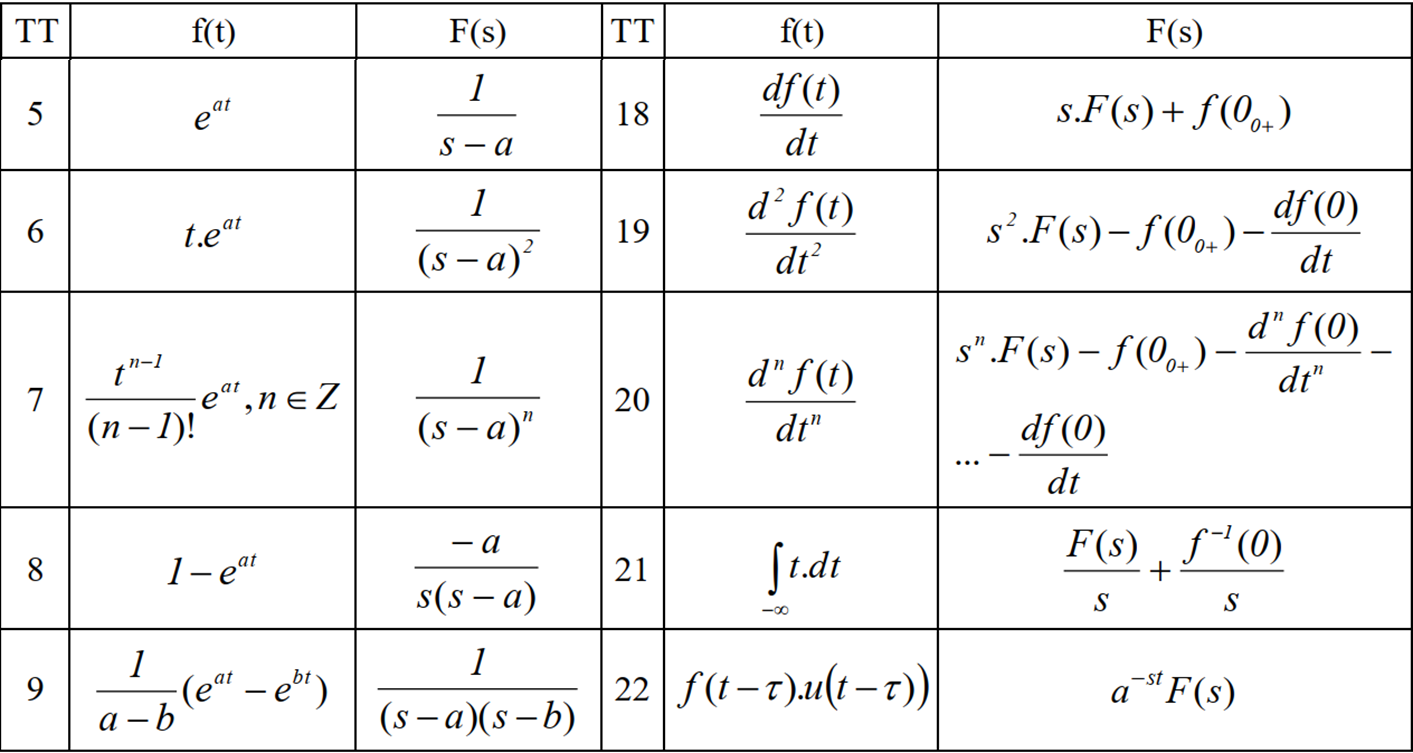
Ghi chú: Sử dụng bảng phải nhân với hàm u(t), hay thỏa mãn điều kiện f(t) = 0 khi t < 0

4.1.2. Hàm truyền
a. Phương trình toán học
Xét hệ thống tuyến tính bất biến liên tục, mô tả bởi phương trình vi phân:
(4.20)
Biến đổi Laplace 2 vế phương trình trên, để ý tính chất ảnh của đạo hàm, giả thiết điều kiện đầu bằng 0, ta được hàm truyền của hệ thống:
(4.21)
Suy ra:
     (2.22)
Đặt:  (2.23)
Vậy: Hàm truyền của hệ thống là tỉ số giữa biến đổi Laplace của tín hiệu ra và biến đổi Laplace của tín hiệu vào khi điều kiện đầu bằng 0
b. Các bước tìm hàm truyền của hệ thống

Bước 1: Thành lập phương trình vi phân mô tả quan hệ vào – ra của phần tử bằng cách:

  - Áp dụng các định luật Kirchoff, quan hệ dòng – áp trên điện trở, tụ điện, cuộn cảm,… đối với các phần tử điện.
  - Áp dụng các định luật Newton, quan hệ giữa lực ma sát và vận tốc, quan hệ giữa lực và biến dạng của lò xo,… đối với các phần tử cơ khí.
  - Áp dụng các định luật truyền nhiệt, định luật bảo toàn năng lượng,… đối với các phần tử nhiệt.

Bước 2: Biến đổi Laplace hai vế phương trình vi phân vừa thành lập ở bước 1, ta được hàm truyền cần tìm.
Chú ý: Đối với các mạch điện có thể tìm hàm truyền theo phương pháp tổng trở phức.